Recommender system for learning SQL using hints
Dejan Lavbič, Tadej Matek and Aljaž Zrnec. 2017. Recommender system for learning SQL using hints, Interactive learning environments (NILE), 25(8), pp. 1048 – 1064.
Abstract
Today’s software industry requires individuals who are proficient in as many programming languages as possible. Structured query language (SQL), as an adopted standard, is no exception, as it is the most widely used query language to retrieve and manipulate data. However, the process of learning SQL turns out to be challenging. The need for a computer-aided solution to help users learn SQL and improve their proficiency is vital. In this study, we present a new approach to help users conceptualize basic building blocks of the language faster and more efficiently. The adaptive design of the proposed approach aids users in learning SQL by supporting their own path to the solution and employing successful previous attempts, while not enforcing the ideal solution provided by the instructor. Furthermore, we perform an empirical evaluation with \(93\) participants and demonstrate that the employment of hints is successful, being especially beneficial for users with lower prior knowledge.
Keywords
Intelligent Tutoring Systems, improving classroom teaching, interactive learning environments, programming and programming languages, recommender system, SQL learning
1 Introduction
Structured query language (SQL) is over three decades old and well-adopted standard, according to ANSI. Most of today’s computing systems depend on efficient data manipulation and retrieval using SQL. The industry is in dire need of software developers and database administrators, proficient in SQL. Most of the SQL language is taught at the undergraduate level of computer science schools and other technical-oriented institutions. However, a typical student, after completing an introductory course of databases, will not possess the required SQL skills (Prior and Lister 2004). The primary reason for this lies in the complexity of the language itself and in the nature of SQL teaching.
Most typically, the students misinterpret certain concepts of the language, such as data aggregation, joins, and filtering using predicates. Another common problem is that the students simply forget database schemas, table and/or attribute names while constructing a query (Mitrovic 2010). (Prior and Lister 2004) recognize in their study that students have difficulties in visualizing the result of their written query, while being graded, if no option for executing query against the database exists. As a consequence, several SQL teaching systems now include a visualization of the database schema, along with the tables and attributes required in the final solution, to help students alleviate the burden of having to remember names. Furthermore, most of the systems also include the option for testing a query and allow students to receive feedback on their solution. Such approaches are merely a convenience for the student, but not a solution to help students conceptualize fundamental parts of the SQL language itself.
Exercises for testing student’s knowledge are usually oriented in a way to check the basic concepts of SQL language, with students receiving lectures beforehand. But once students have to apply the taught concepts on their own, the complexity is overwhelming, unless students have had extensive practice. With the emergence of Intelligent Tutoring Systems (ITS), most computer-aided education systems allow the use of hints to aid the educational process. Some of these systems were also developed for the SQL domain. However, most of such systems encode their knowledge manually, using expert solutions for defining rules and constraints. Therefore, we propose a new system, which is able to offer hints for different steps of the SQL exercise-solving process and requires minimal intervention from experts, making overall process of defining knowledge base for solving SQL problems much quicker and easier, as most of the hints are generated automatically, using past exercise solutions. In addition, our system is able to adapt to the current state the student is in. We also perform evaluation in an actual educational environment to determine the efficiency of the proposed system.
The rest of this paper is organized as follows. The next section provides an overview of ITS and approaches for learning SQL. In Section 3, we provide an extensive description of the proposed system with system’s architecture and the process of hint generation. In Section 4, we perform an empirical evaluation of the proposed system on a group of \(93\) participants with diverse prior knowledge of SQL. We conclude and provide future directions for improving our research in Section 5.
3 Recommender system
3.1 Description of proposed system
We propose a system with intention of helping students solve SQL-related exercises. The system is an extension of a component used in an existing curriculum (Introduction to databases) at University of Ljubljana, Faculty of Computer and Information Science, where students also learn how to formulate correct and efficient SQL queries. The existing component merely automatically evaluates the correctness of a student’s solution by comparing the result set of the student’s query against the result set of an ideal solution (instructor’s solution). Points are then deducted if certain rows or columns are missing from the result matrix or if the order of rows is incorrect. Our system (presented in Figure 3.1) involves the application of hints as a part of student’s problem-solving process. Each student may request multiple hints, provided that the solution given by the student is not empty. The goal of the hint is to either supplement the student’s solution in cases when the student is on the right path, but does not know how to continue, or to offer a new partial solution in cases when the student is moving away from the correct solution. Students have the option to replace their query with the one from the hint or to ignore the hint altogether. The system therefore acts as a query formulator, correcting students’ queries when requested. Hints are formed using solutions from the previous generations of students. The solutions were collected during years \(2012\) and \(2014\) in a process of evaluating student’s SQL skills. Overall the solution pool contained over \(30.000\) entries spread across approximately \(60\) exercises and \(2\) different database schemas (including the well-known northwind database). Each entry was described with the query in plain text format, the final score of the query, user, schema, exercise id and time.
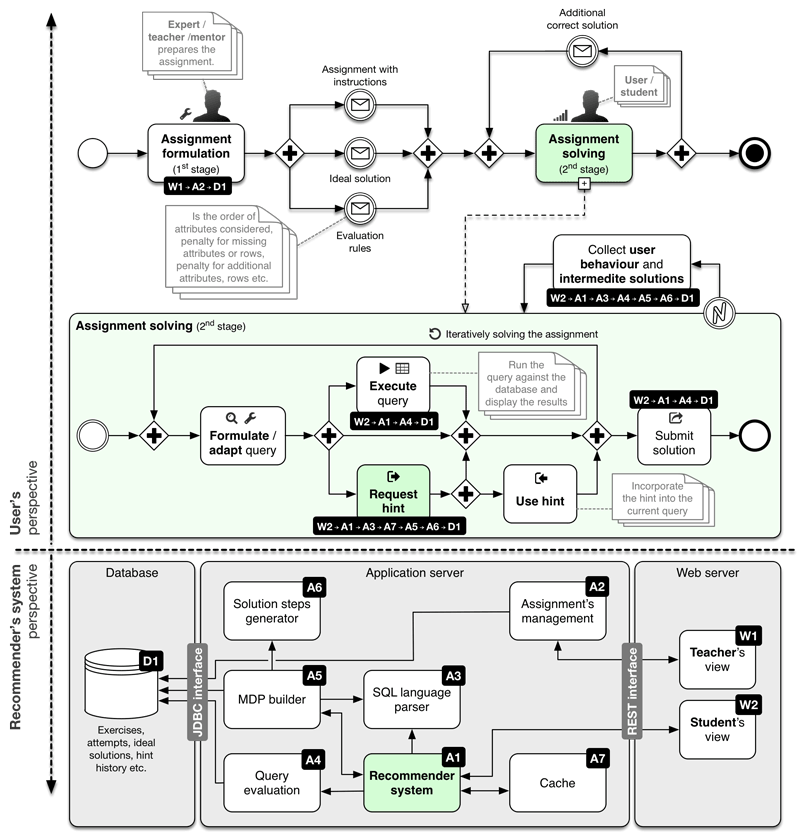
Figure 3.1: Architecture of proposed recommender system from user and system perspective
Figure 3.1 depicts all three major perspectives of the system – the teacher’s view, the student’s view and the system’s view. The process of SQL learning starts with an instructor preparing the exercises to be used for evaluation (assignment formulation). The evaluation rules and ideal solutions need to be provided along with a description of the task and with a representative image of the database schema. Evaluation rules determine the type of scoring used for each exercise, as some exercises may require the student to return rows in a specific order, to name columns in a specific way, etc. Ideal solutions are necessary since exercises may not have matching past (correct) solutions to rely on for hint generation. They also help address the cold-start problem mentioned later on. In our evaluation, exercises were formulated with unambiguity in mind, that is, there is a single unique result matrix for every exercise, which is \(100\%\) correct. Several ideal solutions were provided per exercise, each returning the same ideal result matrix, but using a different concept of data retrieval (e.g. joining multiple tables, aggregating data and nesting queries). In the second stage, the students solve SQL exercises. Their actions are recorded and their solutions used as data for future generations of hint consumers. During the course of exercise-solving process, the students have the option to test the query and receive the result matrix or to request a hint, which then augments their solution. Once satisfied, the students submit their solution as final.
The basis of the system’s perspective is a set of past attempts (queries) at solving SQL exercises, provided by the students from earlier generations. The historical data contain enough information to create a model, which is capable of generating useful hints. The system utilizes MDPs to model the learning process. MDP is defined as a tuple
\[\begin{equation} \langle \mathcal{S}, \mathcal{A}, \mathcal{P}, \mathcal{R}, \gamma \rangle \tag{3.1} \end{equation}\]where \(\mathcal{S}\) is a finite set of states, \(\mathcal{A}\) a finite set of actions connecting the states, \(\mathcal{P}\) a matrix of transition probabilities, \(\mathcal{R}\) a reward function and \(\gamma\) a discount factor. The system’s behaviour is stochastic, that is, the probability matrix defines, for each action, the probability that this action will actually lead to the desired state. The actions therefore have multiple destinations, with each destination being reachable with a given probability. The reward function specifies, for each state, the reward the agent receives upon reaching this state. Note that the reward can also act as a punishment (negative values). Furthermore, a policy \(\pi\) defines a mapping of states to actions. Each policy completely defines the behaviour of an agent in the system as it specifies which action the agent should take next, given the current state. We can define a value function as
\[\begin{equation} V^{\pi}(s) = \sum_{s'} {P_{ss'}(\mathcal{R}_s + \gamma V^{\pi}(s'))} \tag{3.2} \end{equation}\]The goal of MDPs is to find an optimal policy, which maximizes the value function – the reward the agent receives in the future – over all policies, or equivalently \(V^*(s) = \max\limits_{\pi}(V^{\pi}(s))\). We use value iteration to iteratively compute better estimations of the value function for each state until convergence
\[\begin{equation} V^{*}_{i+1}(s) = \max\limits_{a \in \mathcal{A}}\Big(\mathcal{R}_s + \gamma \sum_{s'}\mathcal{P}^{a}_{ss'} V^{*}_{i}(s')\Big) \tag{3.3} \end{equation}\]The value iteration computes, for each state, its new value, given the outgoing actions of the state. The new value of the current state is its baseline reward (\(\mathcal{R}_s\)) plus the maximum contribution among all actions leading to neighbours. A contribution from following a specific action is equal to the weighted sum of the probability of reaching the action’s intended target and the value of the target (neighbour) from the previous iteration. The discount factor gives priority to either immediate or long-term rewards. Observing equation (3.3), we can notice that when \(\gamma\) is low, the contributions from neighbouring states drop with increasing number of iterations.
Our historical data contain just the timestamp, user identification code and submitted SQL query in plain text format. In order to close the gap between raw data and high-level MDP states, we constructed our own version of SQL language parser (component A3 in Figure 3.1). The tool that proved useful was ANother Tool for Language Recognition (ANTLR) (Parr and Quong 1995). ANTLR takes as an input the grammar, which defines a specific language (a subset of context-free languages is supported by ANTLR), and generates parsing code (Java code in our case). Through the use of grammar and lexer rules, a parser was constructed that converts plain text SQL query into a tree-like structure. An example of query parsing is evident from Figure 3.2, where internal tree nodes represent expressions and leaves represent the actual (terminal) symbols of the query.

Figure 3.2: Example of solution steps construction
The individual solution steps, such as in Figure 3.2, are then directly mapped to states in MDP notation. A single MDP state is therefore a tree. Actions are added among consecutive solution steps while making sure there are no duplicate states. We simplify the MDP construction by allowing each state to have only one outgoing action, however that action leads to multiple states. The probability matrix is calculated as the relative frequency of users that have moved from a certain state to another with regard to all users. The rewards are set only for the final states, that is, the states that represent the final step of the solution. Reward function is defined using the existing query evaluation component (component A4 in Figure 3.1). When the query score is high (\(>95\%\)), the state receives a high reward. In all other cases, the state receives a “negative reward”. This is to prevent offering hints, which are only partially correct. The discount factor was set to \(1,0\), giving priority to long-term rewards. In addition, we add backward actions to all states, to aid the students when they happen to be on the wrong path. Backward actions allow the system to return from an incorrect solution path when the reward of taking the forward action is worse than the reward of taking the backward action. Furthermore, we seed the MDP with ideal solutions to improve the hint generation process (component A2 in Figure 3.2). This partially solves the cold-start problem of new exercises, which do not yet have historical data available for hints, as it allows the students to receive hints leading them to one of the ideal solutions. The resulting MDP is a graph (not necessarily connected). An example of such graph is visible in Figure 3.3.
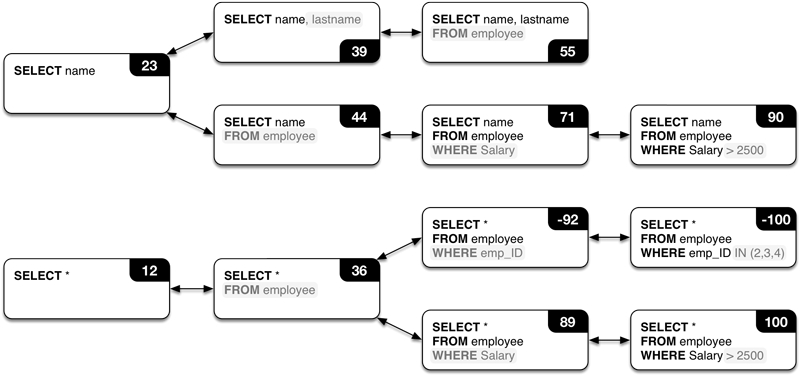
Figure 3.3: Example of MDP graph. The numbers next to the states represent the rewards. The final states are in this case states with rewards \(100\), \(-100\), \(90\) and \(55\)
Let a branch denote one of the paths in one of the connected components of MDP graph, which starts with the first solution step and ends with a final solution. A single branch represents how a single student constructed the solution. When a branch is split, that is, when at a given node of the path/branch, that node leads to multiple other states, then from this point forward, students deviated with their approach to solving this exercise. In cases when the agent is located in an incorrect sub-branch (a path leading to a final incorrect state), the system returns from the incorrect subbranch to the first common ancestor state of both the incorrect sub-branch and an alternative correct branch. Skipping the entire incorrect sub-branch is necessary in order to ensure that hints are progressive. For example, in Figure 3, if an agent was located in a state corresponding to the use of IN clause (state with reward \(-100\) in Figure 3.3), the system would return two steps back and then offer a hint from there.
The hint generation process consists of the following activities (see Figure 3.1). When a student requests a hint, the system accepts the current student’s query as the input in order to match it with one of the states in the MDP graph. The student’s query is parsed into a tree structure and then matched to the most similar state (solution step) in the MDP (component A5 in Figure 3.1). The MDP must be constructed first and because this process is resource intensive (database I/O), we use an in-memory cache (component A7 in Figure 3.1) to store MDPs for each exercise. After the MDP is constructed, we apply value iteration to determine the rewards of remaining, non-final states. Once the MDP is retrieved and the matching state found, the hint is constructed using the next best state given the matching state. This includes converting the solution step into a text representation. An example of hint construction is visible in Table 3.1. The first row of Table 3.1 corresponds to a scenario, where the student is located in an incorrect MDP branch. Observe that the system does not direct the student towards the ideal solution (one of the ideal solutions actually), but proposes an alternative MDP branch, which eventually leads to the correct solution. The alternative MDP branch was constructed by another student’s solution from the previous generation. The last hint in the first row demonstrates that nested queries are also supported. The second row of Table 3.1 corresponds to a scenario, where the student’s solution is partially correct, yet the student fails to continue. As one can observe, the student forgot to include the department table, which is what the hint corrects. A visual example of how the hints are presented can be seen in Figure 3.4.
| Task description | Ideal solution | Student’s solution | Hints |
|---|---|---|---|
| Return the number of employees in department “SALES” |
SELECT COUNT(*) FROM employee, department WHERE employee.dept_ID = department.dept_ID AND department.name = “SALES” |
SELECT * FROM department |
SELECT COUNT(*) FROM department WHERE dept_ID SELECT COUNT(*) FROM department WHERE dept_ID IN (SELECT dept_ID) |
| Return the number of employees in region “DALLAS” |
SELECT COUNT(*) FROM employee e, department d, location l WHERE e.dept_ID = d.dept_ID AND d.loc_ID = l.loc_ID AND region = “DALLAS” GROUP BY region |
SELECT COUNT(e.emp_ID) FROM employee e, location l WHERE region = “DALLAS” |
SELECT COUNT(e.emp_ID) FROM employee e, location l, department d |
So far we have not mentioned how is the state matching actually performed. Because all SQL queries are represented using tree structures, we perform the matching using a tree distance criterion. More specifically we employ the Zhang–Shasha algorithm (Zhang and Shasha 1989), which performs tree distance calculation for ordered trees. There are several improvements we had to consider to make the distance metric feasible. The SQL queries mostly contain aliases, which help the user distinguish two instances of the same table. Because aliases do not follow any syntax, they usually differ from user to user, thus increasing the distance between trees. To alleviate the problem, we perform alias renaming before matching the states. The process renames all aliases to a common name, improving matching. In addition, the Zhang–Shasha algorithm only performs distance calculation for ordered trees. SQL queries are represented using unordered trees, as the order of, for example, selected tables is irrelevant with respect to the final solution. Tree distance for unordered trees is known to be an NP-hard problem. Because trees representing queries are relatively small, we are able to perform unordered tree distance calculation by treating children of certain nodes as unordered sets and then defining a distance metric for comparing the sets. The set distance calculation involves recursively calculating the tree distance for each pair of elements from both sets.
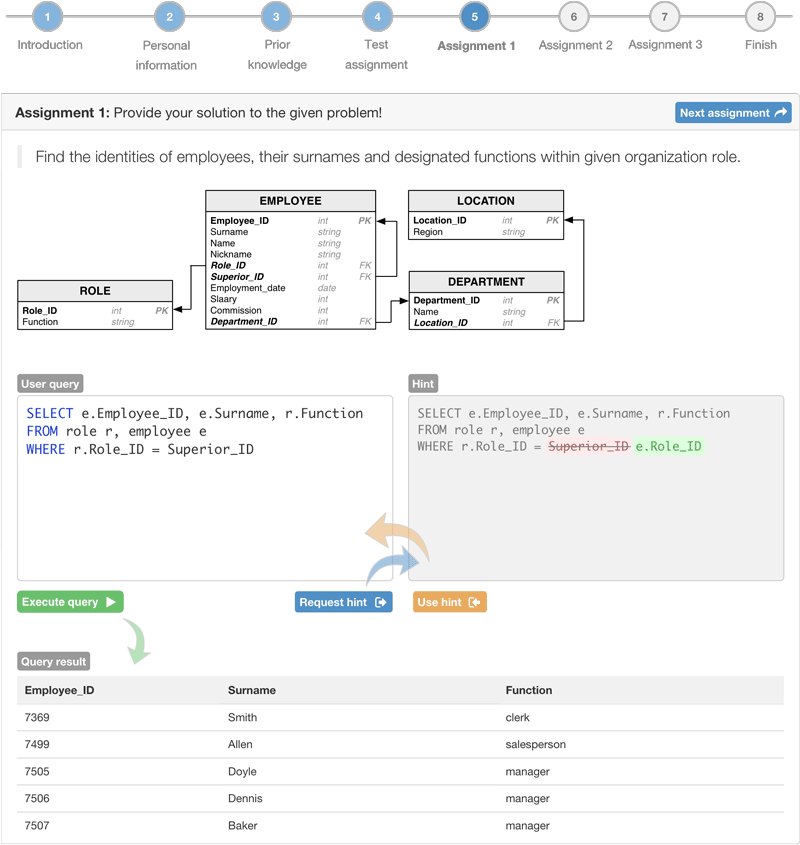
Figure 3.4: Recommender system’s user interface
3.2 Limitations
The strict matching of tree structures may in some scenarios cause problems. Several small changes to the query can reduce the system’s ability to find a matching state and offer a hint. Even though we have implemented several additional mechanisms to alleviate the problem (alias renaming, unordered matching) there are still certain issues due to inputs not following a specific syntax. A simple example is attribute renaming (AS keyword), for exercises where the output needs to follow specific naming rules. In general, we need to handle all cases of free-form user input.
Another limitation of the system is the fact that all hints strictly follow a predefined order of query construction. This is due to the lack of solution steps and our assumption that students construct their query in order of sections (SELECT clause first, then FROM clause, etc.). The system, as a result, does not support hint delivery for arbitrary order of query construction. Instead, the students are expected to construct their queries by the sections of the query.
A potential problem is also the low reward of a certain state even though the state might be a part of the correct solution path. The case when a lot of students moved from a correct state to an incorrect path (when there is an action with high probability leading to a state with low reward) is reflected directly in the system’s ability to offer a hint. Such state will also have a low reward after value iteration even though it is a part of a correct path. However, it is also a part of the incorrect path and is more likely to lead to incorrect solutions. The hints will, because of this, lead to other paths, leaving this state unexplored.
All of the mentioned limitations do not have a major impact on the learning outcome of the system and its ability to deliver hints. As we show in the next section, the effectiveness of the system is more than satisfactory.
4 Evaluation
4.1 Method
The recommender system was implemented as a web application that participants accessed using one of the modern web browsers. The process of providing hints during solving the SQL assignments was evaluated on a group of \(93\) participants, where each of them completed \(3\) assignments, resulting in \(279\) solutions.
During the experiment, before participants started working on assignments, they provided some information about their prior knowledge (SQL proficiency level, years of experience in SQL) to enable clustering and detailed analysis of participants. To obtain diversity of participants’ prior knowledge we employed \(60\) undergraduate students at University of Ljubljana, Faculty of Computer and Information Science with right-skewed prior knowledge and \(33\) more experienced participants in using SQL with left-skewed prior knowledge, resulting in a nearly normal distribution of participants’ prior knowledge (self-reported SQL proficiency and years of experience).
All of the participants’ actions on the web site were recorded for further analysis of the system employment. That allowed us to analyse participant’s time spent on reading instructions, solving the assignment, time spent out of focus with the main window of the assignment and the number of lost focuses. Furthermore, partial query results, distance to correct solution, number of branches and if participant is in the MDP branch, corresponding to a correct solution path were also recorded to construct the participant timeline in solving individual assignment.
Each participant was required to provide a solution to three randomly selected SQL assignments. Each of the assignments was classified into a category based on the difficulty level, where every participant was randomly allocated one easy (selection of attributes from one table and filtering with simple predicates), one moderate (using join to merge data from multiple tables and filtering with more advanced predicates) and one difficult (using nested queries, grouping and aggregation functions) assignment.
As Figure 3.4 depicts, every assignment consisted of instructions, a graphical view of the conceptual model, a query box for entering the solution, an optional hint box and interactive results of the user’s query.
Participants generally first enter a query into the user’s query box and interactively evaluate the results by pressing the “Execute query”" button. At some point, if the participants were unable to continue, they requested a hint from the recommender system, which was then displayed next to the user query with indicated adaptations of the current query (added elements in green colour and removed elements in red colour) (see Figure 3.4). If participants found the hint beneficial, they could instantly employ it by clicking the “Use hint” button. Then the participant could again check the results of their current query by executing it. When one was satisfied with the result, they could continue to the next assignment. If hints were employed, then the participant indicated the level of suitability of provided hints in additional questionnaire.
Additionally, the group of \(60\) undergraduate students were presented with a direct encouragement - their final result (average score of three random assignments) was considered as a part of study obligations of their degree programme, while \(33\) more experienced participants were only asked to participate for the evaluation purposes.
Every participant could request unlimited number of hints per assignments. To discourage participants to excessive use of hints or even solving the complete assignment with hints only, a small score penalty (inversely proportional to assignment complexity) was introduced for hint employment, which was clearly introduced to the participants before starting the evaluation.
After outlier detecion based on recorded time (instructions reading, solving and unfocussed) and observation of participant’s timelines, \(37\) attempts were excluded from the initial data set. Further analysis of our results was conducted on \(242\) attempts, where we observed the following assignment solving dynamics (including \(95\%\) bootstrapped confidence intervals). The mean time participants spent on reading the assignment’s instructions was \(9s\) \([7s, 10s]\), while the mean time spent on solving the assignment was \(268s\) \([242s, 294s]\). The mean number of requested hints per assignment was \(1,43\) \([1,08, 1,82]\), while \(82\) out of \(242\) (\(33,88\%\)) assignments was solved using at least one hint.
4.2 Results and discussion
To evaluate the performance of proposed recommender system, we cluster participants into five segments, based on prior knowledge and feedback on hint usefulness:
- Segment I: attempts of knowledgeable participants without employing hints,
- Segment II: attempts of not knowledgeable participants without employing hints,
- Segment III: attempts of not knowledgeable participants, not finding hints useful,
- Segment IV: attempts of knowledgeable participants, finding hints useful and
- Segment V: attempts of not knowledgeable participants, finding hints useful.
When observing an individual participant in solving a given assignment, several actions are recorded (e.g. altering current solution, executing query, requesting a hint, employing a hint, losing a focus of the current window with the assignment, etc.). With evaluation of the proposed recommender system, we focus mainly on the distance from the correct solution \(\boldsymbol{dist_{sol}}\) in a given time. The distsol is defined as the minimum number of solution steps required reaching the correct state in the MDP graph, given a current state. The metric is calculated using a simple distance criterion, where states are treated as nodes in a graph and actions as links between states. The breadth-first traversal is used to determine the shortest distances and the minimum of all distances is taken.
We define a linear association
\[\begin{equation} \widehat{dist_{sol}} = \alpha +\beta_{type} \cdot \widehat{t}_{elapsed} \tag{4.1} \end{equation}\]where \(\widehat{dist_{sol}} = \frac{dist_{sol}}{\left \| dist_{sol} \right \|}\), \(\widehat{t}_{elapsed} = \frac{t_{elapsed}}{\left \| t{elapsed} \right \|}\) and type \(\in\) (all, pre_first_hint, post_first_hint, after_hint_avg).
When analysing the results, we focus on the following performance indicators:
- participant’s solving time per assignment,
- number of different branches participant encounters per assignment and
- various regression coefficients of participant timeline, when solving the given assignment:
- \(\beta_{all}\) is based on all participant’s actions,
- \(\beta_{pre\_first\_hint}\) or \(\beta_{pre\_fh}\) is based on actions before the first hint employment,
- \(\beta_{post\_first\_hint}\) or \(\beta_{post\_fh}\) is based on actions after the first hint employment and
- \(\beta_{after\_hint\_avg}\) or \(\beta_{aha}\) is based on consequent actions after each hint employment, with an average over all hint requests.
The following Table 4.1 depicts aggregated mean results per predefined five participants’ segments. When examining the results, we endeavour to obtain as negative b values as possible, which indicate rapid advancement towards correct solution (e.g. minimize distance to correct solution over time) and by doing that measure the effect of hint employment.
| Segment | Prior knowledge | Hints useful | \(\boldsymbol{t_{solving}}\) | \(\boldsymbol{n_{branches}}\) | \(\boldsymbol{\beta_{pre\_fh}}\) | \(\boldsymbol{\beta_{aha}}\) | \(\boldsymbol{\Delta\beta}\) |
|---|---|---|---|---|---|---|---|
| I | Knowledgeable | – | \(228,00\) | \(3,88\) | – | – | – |
| II | Not knowledgeable | – | \(254,17\) | \(4,44\) | – | – | – |
| III | Not knowledgeable | No | \(381,76\) | \(4,65\) | \(-0,47\) | \(-5,67\) | \(-5,20\) |
| IV | Knowledgeable | Yes | \(243,00\) | \(3,60\) | \(-2,00\) | \(-6,36\) | \(-4,27\) |
| V | Not knowledgeable | Yes | \(322,80\) | \(4,42\) | \(-0,85\) | \(-10,76\) | \(-9,89\) |
When observing regression coefficients of participant timeline or the degree of convergence to the final solution, we focus on \(\beta_{pre\_first\_hint}\), \(\beta_{after\_hint\_avg}\) and \(\Delta\beta = \beta_{after\_hint\_avg} - \beta_{pre\_first\_hint}\) to measure the impact of hint employment. The aforementioned metrics can be calculated only for segments III, IV and V, as participants from segments I and II did not employ hints (see Table 4.1).
Figure 4.1 depicts a sharp decline in the degree of convergence to the final solution \(\beta\) before and after the hint employment for all segments of participants that employed hints (III, IV and V). The finding is also statistically confirmed by Mann–Whitney–Wilcoxon test for individual segments:
- \(\beta^{III}_{after\_hint\_avg} = -5,67 < \beta^{III}_{pre\_first\_hint} = -0,47\) with \(W^{III} = 73\) and \(p^{III} = 7,2 \times 10^{-3}\),
- \(\beta^{IV}_{after\_hint\_avg} = -6,36 < \beta^{IV}_{pre\_first\_hint} = -2,00\) with \(W^{IV} = 60\) and \(p^{IV} = 2,6 \times 10^{-2}\) and
- \(\beta^{V}_{after\_hint\_avg} = -10,75 < \beta^{V}_{pre\_first\_hint} = -0,85\) with \(W^{V} = 468\) and \(p^{V} = 9,8 \times 10^{-8}\).
We can conclude that the hint, provided by the recommender system, is statistically significant in terms of the impact on the degree of convergence to the final solution as \(\beta_{after\_hint\_avg}\) values of all three segments are significantly lower than \(\beta_{pre\_first\_hint}\).
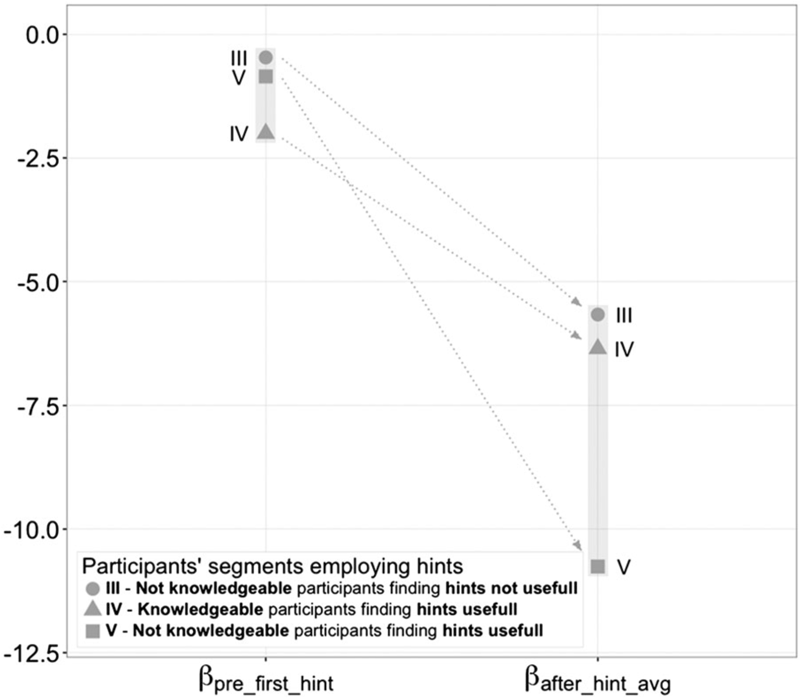
Figure 4.1: Degree of convergence to the final solution \(\beta\)
When considering the magnitude of hint employment impact from Figure 4.1, we can observe \(\Delta\beta = \beta_{after\_hint\_avg} - \beta_{pre\_first\_hint}\) in Figure 4.2. The results show that participants in segments V, III and IV respectively found the provided hints most beneficial. The biggest impact of hint employment on the degree of convergence to the final solution Db can be observed in not knowledgeable participants, finding hints useful (segment IV), which is what was also expected prior evaluation, under assumption that the recommender system would be effective. Similar effects can be observed with knowledgeable participants, finding hints useful (segment V), but the effect size is lower, but still significant. More intriguing finding is that the positive impact of hints employment can also be observed in not knowledgeable participants, not finding hints useful (segment III). Even though participants indicated that hints are not useful, the results show that their advancement towards correct solution, after employing hints was significantly better than before employing hints.
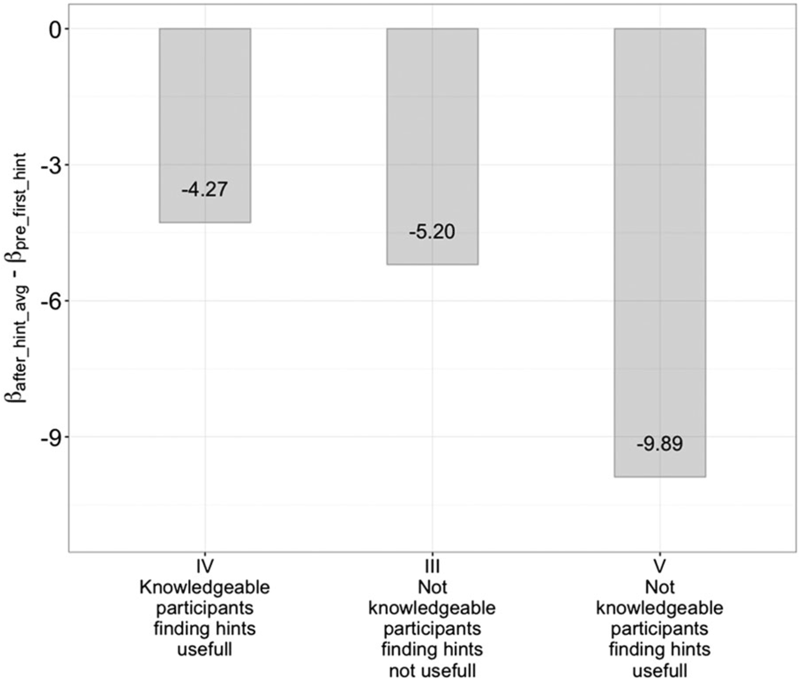
Figure 4.2: Impact of hint employment
To examine the impact of prior knowledge, even further we studied the impact of prior knowledge in hint employment considering assignment solving time (\(t_{solving}\)) and number of different branches (\(n_{branches}\)) in Figure 4.3. Assignment solving time includes only time designated to solving (without instructions reading time and unfocussed time), while number of different branches defines the number of branches participant was designated for in MDP, when solving the SQL assignment. The higher values of nbranches indicate participant exploring significantly different paths to the correct solution and usually not knowing how to continue.
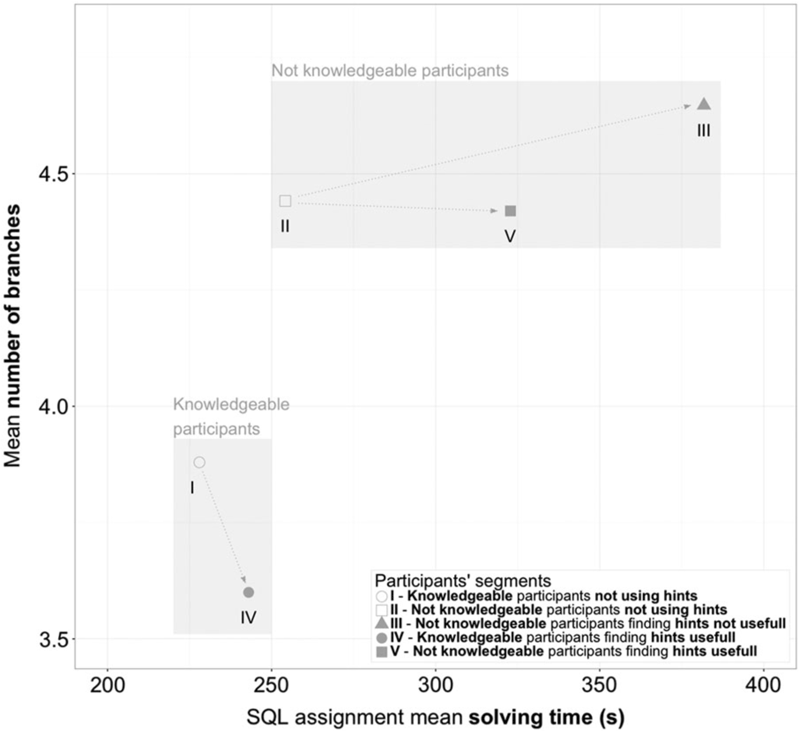
Figure 4.3: Impact of prior knowledge in hint employment
Figure 4.3 depicts that we can, based on \(t_{solving}\) and \(n_{branches}\), cluster together segments I and IV (knowledgeable participants) and segments II, III and V (not knowledgeable participants). The general observation is that knowledgeable participants on average tend to spend less time solving SQL assignments, and are related to lower number of branches than not knowledgeable participants. The arrows in Figure 4.3 indicate the influence of hint employment. We can observe that when knowledgeable participants (segments I an IV) employ hints, \(t_{solving}\) increases but the \(n_{branches}\) decreases, indicating that the number of different paths to the correct solution drops, resulting in more consistent progressing towards final solution. In case of not knowledgeable participants (segments II, III and V), the impact of hints increases \(t_{solving}\), while \(n_{branches}\) slightly decreases when participants find hints useful (segment V) and increases when participants do not find hints useful (segment III).
To further investigate the differences between five segments of participants, Figure 4.4 details the most representational participant of every cluster segment that is the most similar to the median values of the characteristics of performance indications \(t_{solving}\), \(n_{branches}\), \(\beta_{pre\_first\_hint}\), \(\beta_{after\_hint\_avg}\) and \(\Delta\beta\). Figure 4.4 depicts the timeline of representational participant solving the assignment with every recorded action, where hint employment is highlighted (blue dots). Additionally, three regression lines and coefficients are also depicted, based on the following filtering:
- \(\beta_{all}\) for all actions,
- \(\beta_{pre\_first\_hint}\) for actions before first hint employment and
- \(\beta_{post\_first\_hint}\) for actions after the first hint employment.
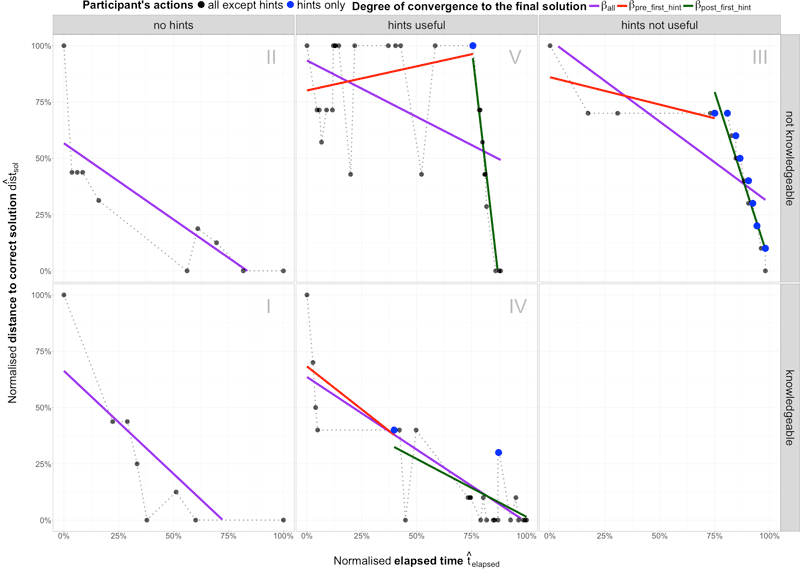
Figure 4.4: Medoids of participant’s timeline
When considering segment I (knowledgeable participants without employing hints) and segment II (not knowledgeable participants without employing hints), we can observe that both groups did not employ hints, hence only ball is depicted. The average participant in segment II is not knowledgeable and he experienced more fluctuations in his path to the final solution than knowledgeable participant in segment I.
When observing participants in segment III (not knowledgeable participants, not finding hints useful), we can conclude that the average participant is able to solve the SQL assignment to certain degree, but then does not know how to continue. At that point, the participant starts requesting hints, which he/she does not find useful. Nevertheless, the hints still lead participant’s current solution to the correct final solution that is the most similar to his/her previous steps in the attempt.
We would like to emphasize attempts in segment IV (knowledgeable participants, finding hints useful) and segment V (not knowledgeable participants, finding hints useful) that both include attempts where participants found hints useful and recommender system provides the most beneficial results, as the impact of hint employment is evident. The average knowledgeable participant from segment IV is able to solve the SQL assignment but is at some points uncertain whether he/she is on the correct path. In that case he/she employs hints, which confirm his/her previous steps and guide him/her to the correct final solution. The average not knowledgeable participant from segment V is at some point unable to continue and after hint employment he/she experience the boost in terms of rapid decline of a distance to correct solution \(\widehat{dist_{sol}}\).
5 Conclusions and future work
In this study, we set out to construct a system to help students learn SQL. The system makes use of past student attempts at solving SQL-related exercises. We employed MDPs to encode the knowledge from historical data and to traverse the states to find the most suitable hint. We parse the SQL language and generate the solution steps in order to close the gap between raw queries and MDP states. We also seed the system with additional expert solutions to improve our ability to deliver a hint.
We tested our system in an actual learning environment. The results indicate that the hints are well accepted and drastically reduce the distance to correct solution even after several steps upon using the hint. If a student’s distance to correct solution alternates before requesting a hint, it is more stable after receiving a hint. The goal of the hints is not merely to improve the overall score of the student, but has a broader intent. If a student does not know how to proceed, they receive a hint, which in turn proposes a new approach to solving a problem. The students therefore explore alternative paths, which they would not consider on their own. This is also why initially, after receiving a hint, some students still alternate with regard to the distance to correct solution, as they are exploring the unfamiliar states and perform errors doing so. As expected, the system has the largest impact on students with low prior knowledge, which is desired.
Our system would benefit from certain improvements in the future. An obvious improvement might be to perform matching of the states not through comparison of tree structures, but rather using a more high-level approach. We could, for example, detect key concepts from every query and then count the number of common concepts whilst comparing two queries. This would also allow discarding any free-form user input from comparison. Another improvement we will consider in the future is to abandon the assumption that the students solve the problems by the order of sections of the query. In order to do that, we would first have to gather new historical data, which also contains steps of query construction. Afterwards, hints could be employed for an arbitrary query construction permutation.
References
Aleven, Vincent, Bruce M. McLaren, Jonathan Sewall, and Kenneth R. Koedinger. 2009. “A New Paradigm for Intelligent Tutoring Systems: Example-Tracing Tutors.” International Journal of Artificial Intelligence in Education 19 (2): 105–54.
Anderson, J. R., A. T. Corbett, K. R. Koedinger, and R. Pelletier. 1995. “Cognitive Tutors: Lessons Learned.” Journal of the Learning Sciences 4 (2): 167–207.
Anderson, John R. 1983. The Architecture of Cognition. Cambridge, MA: Harvard University Press.
Arnau, D., M. Arevalillo-Herraez, and J. A. Gonzalez-Calero. 2014. “Emulating Human Supervision in an Intelligent Tutoring System for Arithmetical Problem Solving.” IEEE Transactions on Learning Technologies 7 (2): 155–64.
Barnes, Tiffany Michelle, John C. Stamper, Lorrie Lehman, and Marvin Croy. 2008. A Pilot Study on Logic Proof Tutoring Using Hints Generated from Historical Student Data.
Bloom, Benjamin S. 1984. “The 2 Sigma Problem: The Search for Methods of Group Instruction as Effective as One-to-One Tutoring.” Educational Researcher 13 (6): 4–16.
Chen, Lin, Barbara Di Eugenio, Davide Fossati, Stellan Ohlsson, and David Cosejo. 2011. Exploring Effective Dialogue Act Sequences in One-on-One Computer Science Tutoring Dialogues. Association for Computational Linguistics.
Chi, M. T. H. 2009. “Active-Constructive-Interactive: A Conceptual Framework for Differentiating Learning Activities.” Topics in Cognitive Science 1 (1): 73–105.
Chi, M., K. VanLehn, D. Litman, and P. Jordan. 2011. “Empirically Evaluating the Application of Reinforcement Learning to the Induction of Effective and Adaptive Pedagogical Strategies.” User Modeling and User-Adapted Interaction 21 (1-2): 137–80.
Eugenio, Barbara Di, Davide Fossati, Susan Haller, Dan Yu, and Michael Glass. 2008. “Be Brief, and They Shall Learn: Generating Concise Language Feedback for a Computer Tutor.” Int. J. Artif. Intell. Ed. 18 (4): 317–45.
Eugenio, Barbara Di, Davide Fossati, Dan Yu, Susan Haller, and Michael Glass. 2005. Aggregation Improves Learning: Experiments in Natural Language Generation for Intelligent Tutoring Systems. Association for Computational Linguistics.
Evens, Martha, and Joel Michael. 2006. One on One Tutoring by Humans and Computers. Psychology Press.
Ezen-Can, Aysu, and Kristy Elizabeth Boyer. 2013. In-Context Evaluation of Unsupervised Dialogue Act Models for Tutorial Dialogue.
Fossati, D., B. Di Eugenio, C. W. Brown, S. Ohlsson, D. G. Cosejo, and L. Chen. 2009. “Supporting Computer Science Curriculum: Exploring and Learning Linked Lists with iList.” IEEE Transactions on Learning Technologies 2 (2): 107–20.
Fossati, D., B. Di Eugenio, S. Ohlsson, C. Brown, and L. Chen. 2015. “Data Driven Automatic Feedback Generation in the iList Intelligent Tutoring System.” Technology, Instruction, Cognition & Learning 10 (1): 5–26.
Fossati, Davide, Barbara Di Eugenio, Christopher Brown, and Stellan Ohlsson. 2008. “Learning Linked Lists: Experiments with the iList System.” In Intelligent Tutoring Systems: 9th International Conference, ITS 2008, Montreal, Canada, June 23-27, 2008 Proceedings, edited by Beverley P. Woolf, Esma Aïmeur, Roger Nkambou, and Susanne Lajoie, 80–89. Berlin, Heidelberg: Springer Berlin Heidelberg.
Fossati, Davide, Barbara Di Eugenio, Stellan Ohlsson, Christopher Brown, Lin Chen, and David Cosejo. 2009. I Learn from You, You Learn from Me: How to Make iList Learn from Students. IOS Press.
Jeong, H., and M. T. H. Chi. 2007. “Knowledge Convergence and Collaborative Learning.” Instructional Science 35 (4): 287–315.
Koedinger, Kenneth R., John R. Anderson, and William H. Hadley. 1997. “Intelligent Tutoring Goes to School in the Big City.” International Journal of Artificial Intelligence in Education 8: 30–43.
Kunmar, Amruth N. 2002. Model-Based Reasoning for Domain Modeling, Explanation Generation and Animation in an ITS to Help Students Learn C++.
Lehman, Blair, Sidney D’Mello, Whitney Cade, and Natalie Person. 2012. “How Do They Do It? Investigating Dialogue Moves Within Dialogue Modes in Expert Human Tutoring.” In Intelligent Tutoring Systems: 11th International Conference, ITS 2012, Chania, Crete, Greece, June 14-18, 2012. Proceedings, edited by Stefano A. Cerri, William J. Clancey, Giorgos Papadourakis, and Kitty Panourgia, 557–62. Berlin, Heidelberg: Springer Berlin Heidelberg.
Melia, M., and C. Pahl. 2009. “Constraint-Based Validation of Adaptive E-Learning Courseware.” IEEE Transactions on Learning Technologies 2 (1): 37–49.
Mitrovic, A., B. Martin, and P. Suraweera. 2007. “Intelligent Tutor for All: The Constraint-Based Approach.” IEEE Intelligent Systems 22 (4): 38–45.
Mitrovic, A., P. Suraweera, B. Martin, and A. Weersinghe. 2004. “DB-Suite: Experiences with Three Intelligent, Web-Based Database Tutors.” Journal of Interactive Learning Research 15 (4): 409–32.
Mitrovic, Antonija. 1998. “Learning SQL with a Computerized Tutor.” ACM SIGCSE Bulletin 30 (1): 307–11.
———. 2010. “Modeling Domains and Students with Constraint-Based Modeling.” In Advances in Intelligent Tutoring Systems, edited by Roger Nkambou, Jacqueline Bourdeau, and Riichiro Mizoguchi, 63–80. Berlin, Heidelberg: Springer Berlin Heidelberg.
Mitrovic, Antonija, and Stellan Ohlsson. 2006. “Constraint-Based Knowledge Representation for Individualized Instruction.” Computer Science and Information Systems 3: 1–22.
Mitrovic, Antonija, Stellan Ohlsson, and Devon K. Barrow. 2013. “The Effect of Positive Feedback in a Constraint-Based Intelligent Tutoring System.” Computers & Education 60 (1): 264–72.
Parr, T. J., and R. W. Quong. 1995. “ANTLR - A Predicated-LL(k) Parser Generator.” Software-Practice & Experience 25 (7): 789–810.
Person, Natalie, Laura Bautista, A. C. Graesser, and Eric Mathews. 2001. Evaluating Student Learning Gains in Two Versions of AutoTutor. Artificial Intelligence in Education: AI-ED in the Wired and Wireless Future. Amsterdam: IOS Press.
Prior, Julia Coleman, and Raymond Lister. 2004. “The Backwash Effect on SQL Skills Grading.” ACM SIGCSE Bulletin 36 (3): 32–36.
Razzaq, L., J. Patvarczki, S. F. Almeida, M. Vartak, M. Y. Feng, N. T. Heffernan, and K. R. Koedinger. 2009. “The ASSISTment Builder: Supporting the Life Cycle of Tutoring System Content Creation.” IEEE Transactions on Learning Technologies 2 (2): 157–66.
Rothman, Terri, and Mary Henderson. 2011. “Do School-Based Tutoring Programs Significantly Improve Students Performance on Standardized Tests?” Research in Middle Level Education 34 (6): 1–10.
Smith-Atakan, A. Serengul, and Ann Blandford. 2003. “ML Tutor: An Application of Machine Learning Algorithms for an Adaptive Web-Based Information System.” International Journal of Artificial Intelligence in Education 13: 235–61.
Stamper, John C., Tiffany Michelle Barnes, and Marvin Croy. 2011. “Enhancing the Automatic Generation of Hints with Expert Seeding.” International Journal of Artificial Intelligence in Education 21 (1-2): 153–67.
Stein, G., A. J. Gonzalez, and C. Barham. 2013. “Machines That Learn and Teach Seamlessly.” IEEE Transactions on Learning Technologies 6 (4): 389–402.
VanLehn, K. 2011. “The Relative Effectiveness of Human Tutoring, Intelligent Tutoring Systems, and Other Tutoring Systems.” Educational Psychologist 46 (4): 197–221.
VanLehn, K., A. C. Graesser, G. T. Jackson, P. Jordan, A. Olney, and C. P. Rose. 2007. “When Are Tutorial Dialogues More Effective Than Reading?” Cognitive Science 31 (1): 3–62.
VanLehn, Kurt, Collin Lynch, Kay Schulze, Joel A. Shapiro, Robert Shelby, Linwood Taylor, Don Treacy, Anders Weinstein, and Mary Wintersgill. 2005. The Andes Physics Tutoring System: Five Years of Evaluations. IOS Press.
Zhang, Kaizhong, and Dennis Shasha. 1989. “Simple Fast Algorithms for the Editing Distance Between Trees and Related Problems.” SIAM Journal on Computing 18 (6): 1245–62.