Discovering Language of the Stocks
Marko Poženel and Dejan Lavbič. 2019. Discovering Language of Stocks, Frontiers in Artificial Intelligence and Applications - Databases and Information Systems X, 315, pp. 243 - 258, IOS Press.
Abstract
Stock prediction has always been attractive area for researchers and investors since the financial gains can be substantial. However, stock prediction can be a challenging task since stocks are influenced by a multitude of factors whose influence vary rapidly through time. This paper proposes a novel approach (Word2Vec) for stock trend prediction combining NLP and Japanese candlesticks. First, we create a simple language of Japanese candlesticks from the source OHLC data. Then, sentences of words are used to train the NLP Word2Vec model where training data classification also takes into account trading commissions. Finally, the model is used to predict trading actions. The proposed approach was compared to three trading models Buy & Hold, MA and MACD according to the yield achieved. We first evaluated Word2Vec on three shares of Apple, Microsoft and Coca-Cola where it outperformed the comparative models. Next we evaluated Word2Vec on stocks from Russell Top 50 Index where our Word2Vec method was also very successful in test phase and only fall behind the Buy & Hold method in validation phase. Word2Vec achieved positive results in all scenarios while the average yields of MA and MACD were still lower compared to Word2Vec.
Keywords
Stock price prediction, Word2Vec, Japanese candlesticks, Trading strategy, NLP
1 Introduction
Investors and the research community have always found forecasting trends and the future value of stocks an interesting topic. Moderately accurate prediction in stock trends can result in high financial benefits and hedge against market risks (Kumar and Thenmozhi 2006). Given the attractiveness of the research area, the number of successful research papers is still quite low. The main reason is usually that nobody wants to publish an algorithm that solves one of the issues that might be most profitable. One of the reasons could be the fact that investors for a long time accepted the Efficient Market Hypothesis (EMH) (Fama 1960). Hypothesis states that prices immediately incorporate all available information about a stock and only new information is able to change price movements (Cavalcante et al. 2016), so abnormal yields are not possible only based on studying the evolution of stock price’s past behavior (Tsinaslanidis and Kugiumtzis 2014; Ballings et al. 2015).
In the last decades, some economists are skeptical about EMH and sympathetic to the idea that stock prices are partially predictable. Others claim that stock markets are more efficient and less predictable than many recent academic papers would have us believe (Malkiel 2003). Nonetheless, a lot of approaches to forecasting the future stock values have been explored and presented (Cavalcante et al. 2016; Ballings et al. 2015).
The main goal of stock market analysis is to better understand stock market in order to be able to take better decisions. Two the most common approaches for stock market analysis are fundamental (Abad, Thore, and Laffarga 2004) and technical analysis (Taylor and Allen 1992). The biggest difference between these two approaches is in the stock market attributes that are taken into account in the analysis. Fundamental analysis inspects the basic company properties such as: the company size, price / profits ratio, assets, and other financial aspects. Often, the marketing strategy, management policy, and company innovation are also taken into account. Fundamental analysis can be improved by including external, political and economic factors like legislation, market trends and data available on-line (Cavalcante et al. 2016).
On the other hand, technical analysis is not interested in analyzing internal and external characteristics of the company. It rather focuses solely on trading, analyses stock chart patterns and volume of trading, monitors trading activities, leaving out a number of subjective factors. Technical analysis is based on the assumption that all internal and external factors that affect company’s stock price are already indirectly included in the stock price. The tools used by technical analysis are charting, relative strength index, moving averages, on balance volumes and others. Technical analysis is based on historical data to predict future stock trends. With EMH in mind, it could be inferred that this market analysis approach will not be effective. However, several scientific papers published in literature using technical analysis have presented successful approaches in stock prediction (Cavalcante et al. 2016).
With technical analysis focusing only on stock prices, prediction of future stock trends can be translated to pattern recognition problem, where financial data are modelled as time series (Teixeira and Oliveira 2010). As a result, several tools and techniques are available ranging from traditional statistic modelling to computational intelligence algorithms (Cavalcante et al. 2016).
The candlestick trading strategy (Lu and Wu 2011; Nison 1991) is a very popular technical method to reveal the growth and decline of the demand and supply in financial markets. It is one of the oldest technical analyses techniques with origins in \(18^{\text{th}}\) century where it was used by Munehisa Homma for trading with rice. He analysed rice prices back in time and acquired huge insights to the rice trading characteristics. Japanese candlestick charting technique is a primary tool to visualize the changes in a commodity price in a certain time span. Almost every software and on-line charting packages (Jasemi, Kimiagari, and Memariani 2011) available today include candlestick charting technique. Although the researchers are not in complete agreement about its efficiency, many researchers are investigating its potential use in various fields (Prado et al. 2013; Jasemi, Kimiagari, and Memariani 2011; Lu and Shiu 2012; Kamo and Dagli 2009; Lu 2014). To visualize Japanese candlestick at a certain time grain (e.g. day, hour), four key data components of a price are required: starting price, highest price, lowest price and closing price. This tuple is called OHLC (Open, High, Low, Close). When the candlestick body is filled, the closing price of the session was lower than the opening price. If the body is empty, the closing price was higher than the opening price. The thin lines above and below the rectangle body are called shadows and represent session’s price extremes. There are many types of Japanese candlesticks with their distinctive names. Each candlestick holds information on trading session and becomes even more important, when it is an integral part of certain sequence.
The goal of our research is defining a simplified language of Japanese candlesticks from OHLC data. This simplified OHLC language is than used as an input for Word2Vec algorithm (Mikolov, Sutskever, et al. 2013) that can learn the vector representations of words in the high-dimensional vector space. We believe that it is possible to learn rules and patterns using Word2Vec and use this knowledge to predict future trends in stock value. Despite many developed models and predictive techniques, measuring performance of the stock prediction models can present a challenge. For example, Jasemi et al. (Jasemi, Kimiagari, and Memariani 2011) used hit ratio to evaluate the performance of the models but neglected financial success of a model. Therefore, one of the research goals of this paper is also to utilize a simple method for testing the performance of forecasting models, the result of which is the financial success or yield of the tested model.
The remaining paper is organized as follows. Section 2 contains a literature overview. Section 3 is dedicated to a detailed overview of the proposed forecasting model. In Section 4 model evaluation and performance metrics are presented. Section 5 presents the conclusions and future work.
3 Proposed forecasting model
A combination of various machine learning methods in a novel and innovative way was combined in the proposed forecasting model. The basic assumption behind the proposed approach is that Japanese candlesticks are not only powerful tool for visualizing OHLC data, but also contain predictive power (Jasemi, Kimiagari, and Memariani 2011; Lu and Shiu 2012; Kamo and Dagli 2009; Lu 2014).
Various sequences of Japanese candlesticks are used to forecast the value of a stock in our approach. The foundation for stocks’ language (i.e. words) is defined by Japanese candlesticks. A language in general consists of words and patterns of words that can be further grouped into sentences that express some deeper meaning. The proposed model relies on the similarities with the natural language.
In the beginning of the forecasting process, the transformation of OHLC data is performed and results in a simplified language of Japanaese candlesticks, i.e. stocks’ language. The acquired language is then processed with the NLP algorithm Word2Vec (Mikolov, Sutskever, et al. 2013) where we train the model with given characteristics and the legality of the proposed stocks’ language. For predicting future trends in a stock value the trained model is then employed. The approach is depicted in Figure 3.1, with detailed description provided in the following subsections.
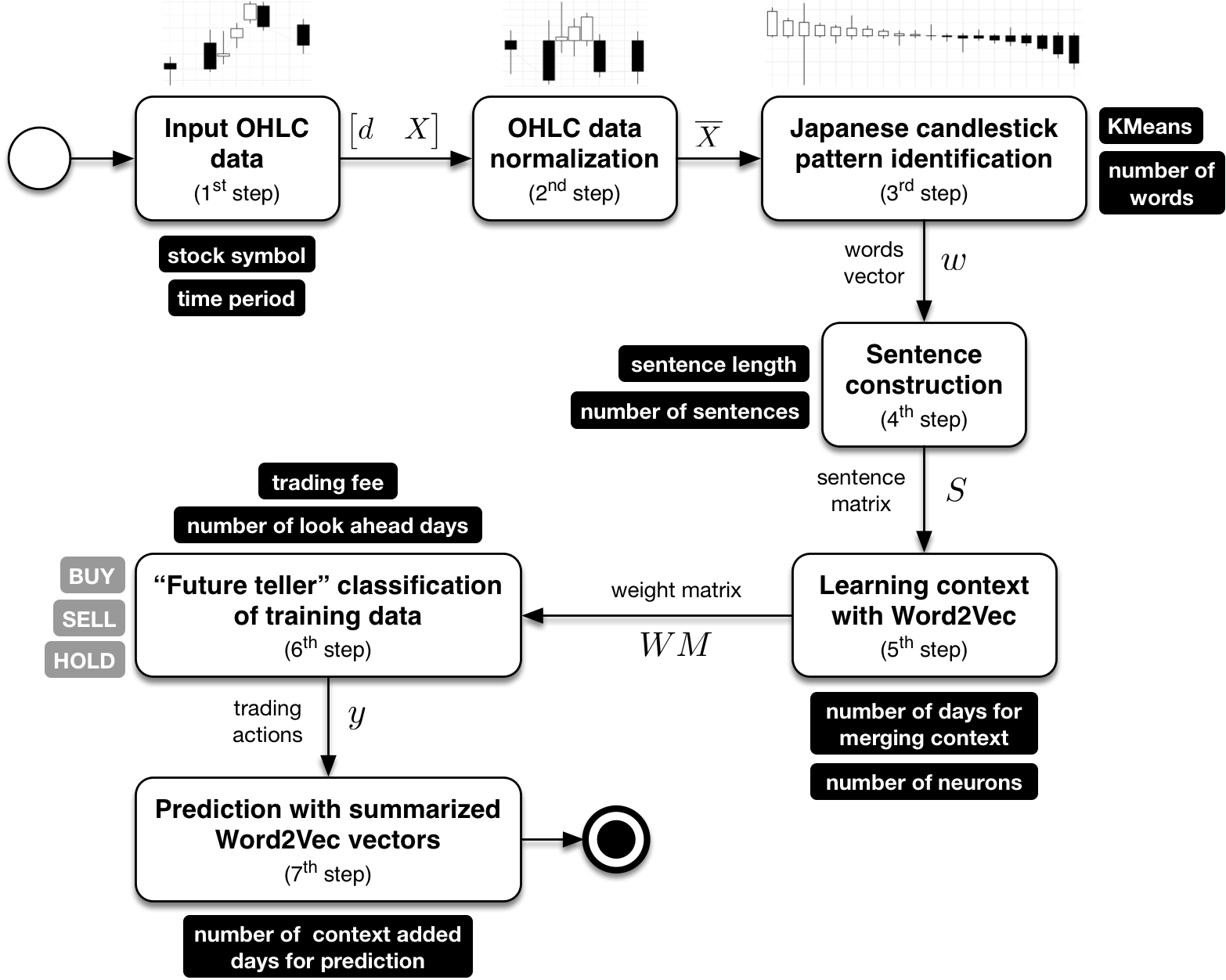
Slika 3.1: Steps of proposed forecasting model
3.1 OHLC data
For a given stock we observe the input data on a trading day basis for \(\boldsymbol{n_d}\) trading days as defined in the following matrix
\[\begin{equation} \begin{bmatrix} d_{(\text{$1$ $\times$ $n_d$})} & X_{(\text{$4$ $\times$ $n_d$})} \end{bmatrix} = \begin{bmatrix} \begin{array}{cc} d_1 \\ d_2 \\ \dots \\ d_{n_d} \end{array} \left| \begin{array}{*{4}c} O_1 & H_1 & L_1 & C_1 \\ O_2 & H_2 & L_2 & C_2 \\ \dots & \dots & \dots & \dots \\ O_{n_d} & H_{n_d} & L_{n_d} & C_{n_d} \end{array} \right. \end{bmatrix} \tag{3.1} \end{equation}\]where \(d_{(\text{$1$ $\times$ $n_d$})}\) is a vector of trading days and \(X_{(\text{$4$ $\times$ $n_d$})}\) is a matrix of OHLC trading data.
OHLC tuples are Japanese candlesticks presentation with individual four attributes that denote absolute value in time. Raw OHLC data in Equation (3.1) are convenient for graphical presentation but are not most suitable for further processing.
3.2 Data normalization
We are interested in the shape of Japanese candlesticks and not an absolute value, so the OHLC tuples were normalized by dividing OHLC data attributes (Open, High, Low, Close) with Open attribute as follows
\[\begin{equation} norm\big(\langle O,H,L,C \rangle\big) = \langle 1, \frac{H}{O}, \frac{L}{O}, \frac{C}{O}\rangle: X \to \overline{X} \tag{3.2} \end{equation}\]The employment of the transformation from Equation (3.2) results in a new input trading data matrix
\[\begin{equation} \overline{X}_{(\text{$4$ $\times$ $n_d$})} = \begin{bmatrix} 1 & \frac{H_1}{O_1} & \frac{L_1}{O_1} & \frac{C_1}{O_1} \\\ 1 & \frac{H_2}{O_2} & \frac{L_2}{O_2} & \frac{C_2}{O_2} \\\ \dots & \dots & \dots & \dots \\\ 1 & \frac{H_{n_d}}{O_{n_d}} & \frac{L_{n_d}}{O_{n_d}} & \frac{C_{n_d}}{O_{n_d}} \end{bmatrix} \tag{3.3} \end{equation}\]where the shape of Japanese candlesticks is retained.
3.3 Word Pattern Identification
The majority of forecasting models employing Japanese candlesticks have a drawback of using predefined shapes of candlesticks (Martiny 2012).
Our approach uses automatic detection of candlestick clusters with unsupervised machine learning methods that were beneficial in previous research (Martiny 2012; Jasemi, Kimiagari, and Memariani 2011).
The reason behind using K-Means clustering was to limit the number of possible OHLC shapes (i.e. words of stocks’ language) while still being able to influence the unsupervised training process by defining selected threshold for maximum number of different words.
In the process we define the maximum number of words in stocks’ language as \(\boldsymbol{n_w}\) and employ K-Means clustering algorithm to transform input data \(\overline{X}\) to vector \(w\) as follows
\[\begin{equation} KMeans\big(n_w\big): \overline{X} \to w \tag{3.4} \end{equation}\]where a word \(w_i\) is defined by an individual trading day \(\overline{X_i}\) and is a representation of a specific Japanese candlestick (the mean value of cluster \(i\)). The result of KMeans clustering is a vector
\[\begin{equation} w_{(\text{$1$ $\times$ $n_d$})} = \begin{bmatrix} w_1 & w_2 & \dots & w_{n_d} \end{bmatrix}^T \tag{3.5} \end{equation}\]where given word \(w_i\) is an element from a set of all possible Japanese candlesticks, where \(i = \big[1,n_w\big]\).
An example of a clustering process for a stock KO (Coca-Cola) is depicted in Figure 3.2, where \(n_w = 20\) was used for maximum number of words. The value of parameter \(n_w\) is based on the Silhouette measure (Rousseeuw 1987), which shows how well an object lies in within a certain cluster (cohesion) compared to other clusters (separation). The Silhouette ranges from -1 to +1, where higher value of average Silhouettes means higher clustering validity. In defining stocks’ language, our aim was also to retain the similarity of words that also exists in natural language by controlling \(n_w\) and the Silhouette measure.
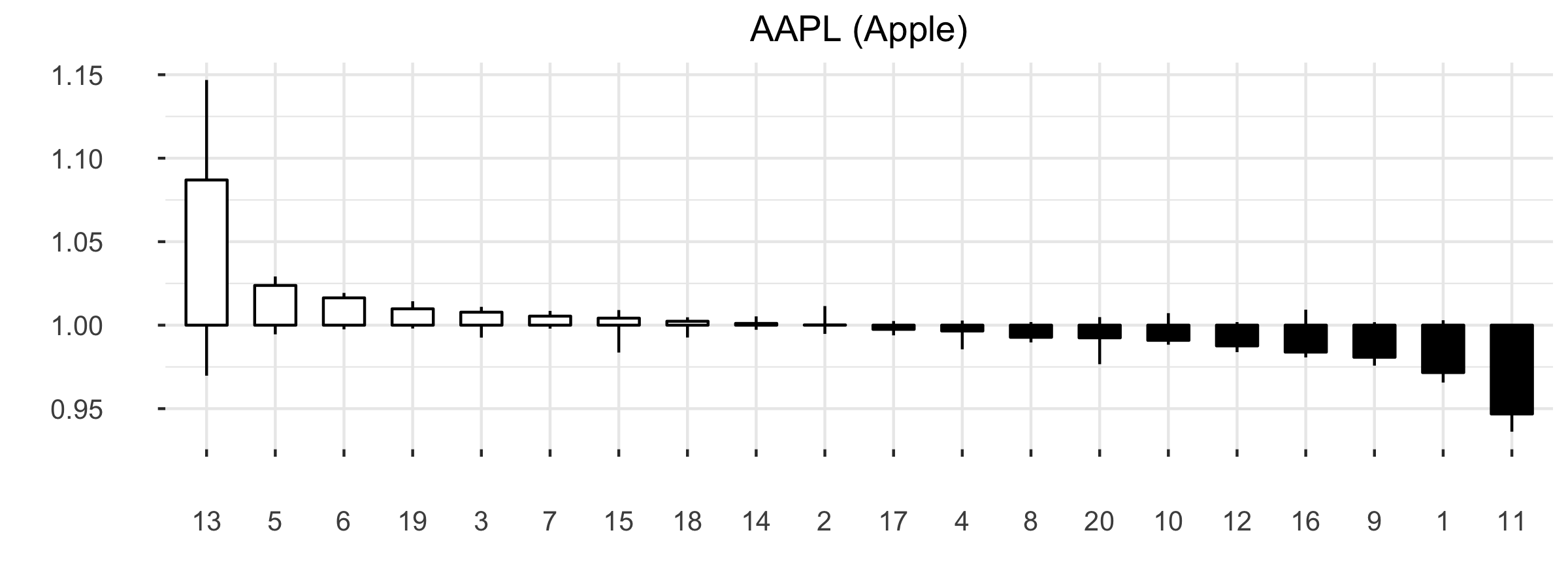
Slika 3.2: Example of \(20\) OHLC pattern clusters for stock AAPL
3.4 From Words to Sentences
With numerous OHLC tuples the potential set of words for the stocks’ language is virtually infinite. In the previous section we have limited this to \(n_w\), which directly influences the performance of the proposed predictive model.
Looking at the analysis of the past movements in the value of stock we can see that Japanese candlesticks’ sequences contain a certain predictive power (Nison 1991; Lu and Shiu 2012). Therefore, we considered past sequences of OHLC as a basis for the stock trend prediction by forming possible sentences in the future.
The rules for forecasting purposes in proposed model are not predefined and are rather constructed from sequences of patterns that are acquired from past movements in stock value.
We specify a sentence length \(\boldsymbol{l_s}\) that defines the number of consecutive words (i.e. trading days) grouped into sentences. The number of sentences \(\boldsymbol{n_s}\) is therefore dependent on the number of trading days \(n_d\) and the sentence length \(l_s\) and is defined as follows
\[\begin{equation} n_s = n_d - (l_s - 1) \tag{3.6} \end{equation}\]The result of the sentence construction process is a sentence matrix \(\boldsymbol{S}\) of rolling windows of trading data (more specifically words in stocks’ language from vector \(w\)) from a transformation \(w \to S\). Sentence matrix \(S\) with \(l_s\) columns (sentence length) and \(n_s\) rows (number of sentences) is further defined as
\[\begin{equation} S_{(\text{$l_s$ $\times$ $n_s$})} = \begin{bmatrix} w_1^{'} & w_2^{'} & \dots & w_{l_s}^{'} \\\ w_2^{'} & w_3^{'} & \dots & w_{l_s + 1}^{'} \\\ \dots & \dots & \dots & \dots \\\ w_{n_s}^{'} & w_{n_s + 1}^{'} & \dots & w_{n_d}^{'} \end{bmatrix} \tag{3.7} \end{equation}\]It seems that this kind of OHLC language is very simple. However, considering the number of possible values for each word \(w_i\), a set of different possible sentences or patterns is enormous. Therefore, the defined language has a high expressive power and is suitable for predictive purposes.
3.5 Word2Vec Training
Based on the patterns in OHLC sentences, the model builds the language context that is then used to perform predictions in the following steps. The system employs historical data, recognizes existing patterns in sentences, learns the context of the words and also renews the context according to new acquired data by employing Word2Vec algorithm (Mikolov, Sutskever, et al. 2013) for training the context.
Word2Vec algorithm with skip-gram (Mikolov, Sutskever, et al. 2013; Mikolov, Chen, et al. 2013) uses a model to represent words with vectors from large amounts of unstructured text data. In the training process, Word2Vec acquires vectors for words that explicitly contain various linguistic rules and patterns by employment of neural network that contains only one hidden level, so it is relatively simple. Many of these patterns can be represented as linear translations. The Word2Vec algorithm has proved to be an excellent tool for analysing the natural language, for example, the calculation
\[vector(\text{'Madrid'}) - vector(\text{'Spain'}) + vector(\text{'Paris'})\]
yields the result that is closer to the \(vector(\text{'France'})\) than any other word vector (Mikolov, Chen, et al. 2013; Mikolov, Yih, and Zweig 2013).
For learning context in financial trading with Word2Vec we define the number of days for merging context \(\boldsymbol{n_{ww}}\) and \(\boldsymbol{n_v}\) in hidden layer weight matrix. Word2Vec algorithm performs the following transformation
\[\begin{equation} W2V\big(S, n_{ww}, n_v\big) : S \to WM \tag{3.8} \end{equation}\]where the result of Word2Vec learning phase is a Weight Matrix \(\boldsymbol{WM}\) with \(n_v\) columns (number of vectors) and \(n_w\) rows (number of words in stocks’ language) and is defined as follows
\[\begin{equation} WM_{(\text{$n_v$ $\times$ $n_w$})} = \begin{bmatrix} v_{1,1} & v_{1,2} & \dots & v_{1,n_v} \\\ v_{2,1} & v_{2,2} & \dots & v_{2,n_v} \\\ \dots & \dots & \dots & \dots \\\ v_{n_w,1} & v_{n_w,2} & \dots & v_{n_w,n_v} \end{bmatrix} \tag{3.9} \end{equation}\]with \(v_{i,j}\) as the \(j\)-th vector (weight) of word \(w_i\).
3.6 Training Data Classification
The proposed model is already capable of using the context that it learned from historical data for creating OHLC predictions. However, our aim is that the predictive model would, based on input OHLC sequence, trigger one of the following actions:
- \(\text{BUY}\),
- \(\text{SELL}\),
- \(\text{HOLD}\) or do nothing.
For prediction of the future stock price we label trading days from matrix \(X\) in training set with trading actions \(\boldsymbol{y}\) where
\[\begin{equation} y_{(\text{$1$ $\times$ $n_d$})} = \begin{bmatrix} A_1 & A_2 & \dots & A_{n_d} \end{bmatrix}^T \tag{3.10} \end{equation}\]and we classify the individual trading day \(y_i\) as \(\text{BUY}\), \(\text{SELL}\) or \(\text{HOLD}\) based on the number of look ahead days \(\boldsymbol{n_{la}}\) and the trading fee \(\boldsymbol{v_{fee}}\) as follows
\[\begin{equation} y_i = \begin{cases} 0 : \text{BUY} & \text{$n_{max} \cdot C_j > n_{max} \cdot C_i + 2 \cdot v_{fee}$, $j \in \big[i, i+n_{la}\big]$} \\ 1 : \text{SELL} & \text{$n_{max} \cdot C_j < n_{max} \cdot C_i - 2 \cdot v_{fee}$, $j \in \big[i, i+n_{la}\big]$} \\ 2 : \text{HOLD} & \text{otherwise} \end{cases} \tag{3.11} \end{equation}\]where \(C_i\) is the stock’s close price of a given trading day \(i\) and \(\boldsymbol{n_{max}} = \big\lceil\frac{e}{C}\big\rceil\) is the maximum number of stocks to trade with \(\boldsymbol{e}\) as the initial equity.
3.7 Performing Prediction
Our proposed model includes classification using the SoftMax algorithm in our Word2Vec neural network (NN). SoftMax regression is a multinomial logistic regression and it is a generalization of logistic regression (see Equation (3.12)). It is used to model categorical dependent variables (e.g. \(\text{$0$ : BUY}\), \(\text{$1$ : SELL}\) and \(\text{$2$ : HOLD}\)) and the categories must not have any order (or rank).
The output neurons of Word2Vec NN use Softmax, i.e. output layer is a Softmax regression classifier. Based on input sequence, SoftMax neurons will output probability distribution (floating point values between \(0\) and \(1\)), and the sum of all these \(V = \{ \text{BUY, SELL, HOLD}\}\) output values (\(y_k\)) will add up to \(1\).
\[\begin{equation} y_k = P(y = k \mid x) = \frac{e^{x^T w_k}}{\sum_{i = 1}^{n_w}{e^{x^T w_i}}} \tag{3.12} \end{equation}\]Excessive increase of the model parameters due to over-fitting of data can also affect the model performance. To minimize the aforementioned problem, we employed least squares regularization that uses cost function which pushes the coefficients of model parameters to zero and hence reduce cost function.
For learning any model we have to omit training days without class prediction, due to look ahead of “Future Teller” from section 3.6, where the corrected number of trading days is \(\boldsymbol{\overline{n_d}} = n_d - n_{la}\).
3.7.1 Basic prediction
When building a basic prediction, we use normalized OHLC data from matrix \(\overline{X}\) (see section 3.2) and vector of trading actions \(y\) from “Future Teller” classification (see section 3.6), where SoftMax classifier defines the following transformation
\[\begin{equation} \begin{bmatrix} \overline{X}_{(\text{$3$ $\times$ $\overline{n_d}$})} & y_{(\text{$1$ $\times$ $\overline{n_d}$})} \end{bmatrix} = \begin{bmatrix} \begin{array}{*{4}c} \frac{H_1}{O_1} & \frac{L_1}{O_1} & \frac{C_1}{O_1} \\\ \frac{H_2}{O_2} & \frac{L_2}{O_2} & \frac{C_2}{O_2} \\\ \dots & \dots & \dots \\\ \frac{H_{\overline{n_d}}}{O_{\overline{n_d}}} & \frac{L_{\overline{n_d}}}{O_{\overline{n_d}}} & \frac{C_{\overline{n_d}}}{O_{\overline{n_d}}} \end{array} \left| \begin{array}{cc} A_1 \\\ A_2 \\\ \dots \\\ A_{\overline{n_d}} \end{array} \right. \end{bmatrix} \to y = f\big(\frac{H}{O}, \frac{L}{O}, \frac{C}{O}\big) \tag{3.13} \end{equation}\]With basic prediction we did not include the context of OHLC candlestics appearance, which influence the price movement and therefore, the prediction did not perform well. In the following step prediction with Word2Vec was performed and taking into account the context by adding previous days OHLC candlesticks.
3.7.2 Word2Vec Prediction with Summarization
From vector of words \(w\) (see Equation (3.5)) and vector of trading actions \(y\) (see Equation (3.10)) in the following format
\[\begin{equation} \begin{bmatrix} w_{(\text{$1$ $\times$ $\overline{n_d}$})} & y_{(\text{$1$ $\times$ $\overline{n_d}$})} \end{bmatrix} = \begin{bmatrix} \begin{array}{cc} w_1 \\\ w_2 \\\ \dots \\\ w_{\overline{n_d}} \end{array} \left| \begin{array}{cc} A_1 \\\ A_2 \\\ \dots \\\ A_{\overline{n_d}} \end{array} \right. \end{bmatrix} \tag{3.14} \end{equation}\]we replace words \(w_i\) with a Word2Vec representation with \(n_v\) features vector (hyper parameter) from Weight Matrix \(WM_{(\text{$n_v$ $\times$ $n_w$})}\) (see Equation (3.9)), where \(w_i = \big[v_{i,1}, v_{i,2}, \dots, v_{i,n_v}\big]\). Training data in a matrix \(X_{(\text{$n_v$ $\times$ $\overline{n_d}$})}^{'}\) is defined as follows
\[\begin{equation} \begin{bmatrix} X_{(\text{$n_v$ $\times$ $\overline{n_d}$})}^{'} & y_{(\text{$1$ $\times$ $\overline{n_d}$})} \end{bmatrix} = \begin{bmatrix} \begin{array}{*{4}c} v_{1,1} & v_{1,2} & \dots & v_{1,n_v} \\\ v_{2,1} & v_{2,2} & \dots & v_{2,n_v} \\\ \dots & \dots & \dots & \dots \\\ v_{w_{\overline{n_d}},1} & v_{w_{\overline{n_d}},2} & \dots & v_{w_{\overline{n_d}},n_v} \end{array} \left| \begin{array}{cc} A_1 \\\ A_2 \\\ \dots \\\ A_{\overline{n_d}} \end{array} \right. \end{bmatrix} \tag{3.15} \end{equation}\]We add context by adding previous \(\boldsymbol{n_m}\) trading days to the current trading day and define a new input matrix \(X_{(\text{$n_v$ $\times$ $\overline{n_d}^{'}$})}^{''}\), where \(\overline{n_d}^{'} = \overline{n_d} - n_m\).
Let \(\boldsymbol{cv_j} = [cv_{1,j}, cv_{2,j}, \dots, cv_{n_v,j}] \in X^{''}\) be a context vector for a given trading day \(j\) (row \(j\) in matrix \(X^{''}\)), where \(j \in [1, \overline{n_d}^{'}]\) and contextualized input matrix \(\boldsymbol{X^{''}}\) is defined as follows
\[\begin{equation} \begin{bmatrix} X_{(\text{$n_v$ $\times$ $\overline{n_d}^{'}$})}^{''} & y_{(\text{$1$ $\times$ $\overline{n_d}^{'}$})} \end{bmatrix} = \begin{bmatrix} \begin{array}{*{4}c} cv_{1,1} & cv_{1,2} & \dots & cv_{1,n_v} \\\ cv_{2,1} & cv_{2,2} & \dots & cv_{2,n_v} \\\ \dots & \dots & \dots & \dots \\\ cv_{w_{\overline{n_d}}^{'},1} & cv_{w_{\overline{n_d}}^{'},2} & \dots & cv_{w_{\overline{n_d}}^{'},n_v} \end{array} \left| \begin{array}{cc} A_1 \\\ A_2 \\\ \dots \\\ A_{\overline{n_d}^{'}} \end{array} \right. \end{bmatrix} \tag{3.16} \end{equation}\]where context vector \(cv_j\) is a sum of vectors of \(n_m\) previous trading days as follows
\[\begin{equation} cv_j = \sum_{k = j}^{j + n_m} v_k \tag{3.17} \end{equation}\]where \(v_k = [v_{1,k}, v_{2,k}, \dots, v_{\overline{n_d},k}]\) is the \(\text{$k$-th}\) row in matrix \(X^{'}\).
4 Evaluation
To summarize the findings of the results for Apple (AAPL), Microsoft (MSFT) and Coca-Cola (KO) shares, the proposed model yielded promising results. In the test phase, the proposed forecast model combined with the proposed trading strategy outperformed all comparative models as depicted in Table 4.1.
| Buy & Hold | MA(50,100) | MACD | W2V | |
|---|---|---|---|---|
| Apple (AAPL) | $102,557.08 | $34,915.34 | $46,452.72 | $182,938.35 |
| Microsoft (MSFT) | -$2,927.03 | -$4,140.42 | -$3,261.15 | $11,109.06 |
| Coca-Cola (KO) | $1,996.82 | $2,066.74 | -$1,108.05 | $4,360.76 |
| Average | $33,875.62 | $10,947.21 | $14,027.84 | $66,136.05 |
In the validation phase, the performance was a bit lower but the average yield of the proposed model was still higher than the comparable models as depicted in Table 4.2. However, drawing conclusions based only on three sample shares may not be meaningful, so we carried out extensive testing on a larger data set and run confirmatory data analysis.
| Buy & Hold | MA(50,100) | MACD | W2V | |
|---|---|---|---|---|
| Apple (AAPL) | $28,611.11 | $32,339.63 | $6,619.31 | $57,543.47 |
| Microsoft (MSFT) | $20,316.42 | $1,809.31 | $2,477.12 | $10,603.90 |
| Coca-Cola (KO) | $5,547.81 | $3,583.26 | -$4,220.57 | $3,163.32 |
| Average | $18,158.45 | $12,577.40 | $1,625.28 | $23,770.19 |
For the final test set we selected stocks from Russell Top 50 Index, which includes 50 stocks of the largest companies (market cap and current index membership) in the U.S stock market. The forecasting model was tested for each stock separately. Thus, for each of the 50 stocks, the prediction model was trained based on past stock values of the particular stock. In the test phase, the model parameters were adjusted that the model achieved highest yield for particular stock. The trained model with parameters tuned for the particular stock was then tested on validation set. Table 4.3 shows average yield achieved by the proposed Word2Vec (W2V) model as well as yield achieved by comparative models (Buy & Hold, Moving Average and MACD) for the test and validation phase. In the test phase, average yield of the proposed W2V model was much higher than yield of the comparative models. However, in the validation phase the results were not as good as in the test phase. The average yield of Moving Average and MACD models were still smaller, while Buy & Hold outperformed our model.
| Buy & Hold | MA(50,100) | MACD | W2V | |
|---|---|---|---|---|
| Russell Top 50 Index - Test phase | $2,818.98 | $1,073.06 | -$482.04 | $11,725.25 |
| Russell Top 50 Index - Validation phase | $16,590.83 | $6,238.43 | $395.10 | $10,324.24 |
A more detailed results for individual stocks at the test phase is presented in Table 4.4. In the test phase, our model generates profit for all except one stock (i.e. JNJ), where zero profit is achieved. What is more, our model outperformed the comparative models in all but three cases (stocks SLB, DIS and JNJ). In the validation phase, the results are worse but still encouraging. Only in \(14\%\) of cases the model gave negative yield, while in \(16\%\) cases the model outperformed all comparative models. In \(30\%\) of cases the model was the second best model. What is more, in \(7\) cases the model’s yield was very close to the yield of the best method.
Average yield gives us some information about the model’s performance. However, based on average yield we are unable to conclude whether the proposed model yields statistically significant better results than comparative models. To get statistically significant results, we carried out statistical tests. We have two nominal variables: forecasting model (e.g. Buy & Hold vs. W2V) and individual stock (e.g. IBM, AAPL, MSFT, GOOGL etc.) and one measurement variable (stock yield). We have two samples in which observations in one sample is paired with observations in the other sample. A paired t-test is used to compare two population means when the differences between pairs are normally distributed. In our case the population data does not have a normal distribution. What is more, distribution of differences between pairs is severely non-normally distributed (the differences in yield for stocks are substantial). In such cases, Wilcoxon signed-rank test is used. The null hypothesis for this test is that the medians of two samples are equal (e.g. Buy & Hold vs. W2V). We determined the statistical significance with the help of z-score, that is calculated based on the Equation (4.1):
\[\begin{equation} z \approx \frac{W - \frac{N (N + 1)}{4}}{\sqrt{\frac{N (N + 1) (2N + 1)}{24}}} = \frac{W - 637.5}{103.591} \tag{4.1} \end{equation}\]where \(N = 50\) denotes sample size (number of stocks) and \(W\) denotes test statistics. Test statistics \(W = \min(W^{-}, W^{+})\), where \(W^{-}\) denotes sum of the ranks of the negative differences and \(W^{+}\) sum of the ranks of the positive differences (how many times the yield of the first method is higher than the yield of the second method). For the calculated z-value we look up in the normal probability table (z-table) for the corresponding p-value. We accept our hypothesis for p-values which are less than \(0.05\).
| Buy & Hold | MA(50,100) | MACD | W2V | |
|---|---|---|---|---|
| VZ | -$3.039,61 | $647,66 | -$2.990,29 | $3.080,84 |
| T | -$359,55 | -$42,32 | -$1.280,35 | $8.273,56 |
| UNH | -$3.769,27 | -$288,51 | -$3.398,75 | $5.050,80 |
| AMGN | -$291,37 | $252,85 | $3.227,64 | $7.668,43 |
| GE | -$3.927,61 | -$2.472,75 | -$3.128,26 | $2.956,75 |
| CELG | $25.708,81 | $5.608,72 | $12.781,08 | $50.882,06 |
| CMCSA | -$542,23 | $982,66 | -$2.407,12 | $2.889,15 |
| KO | $2.519,05 | $3.778,97 | -$1.866,26 | $5.813,29 |
| MCD | $8.955,17 | $1.114,14 | $898,75 | $12.868,28 |
| AGN | $3.441,65 | $2.536,50 | $747,18 | $5.693,08 |
| QCOM | -$772,94 | $1.228,42 | -$3.761,31 | $9.237,34 |
| SLB | $11.208,42 | $8.533,32 | $596,46 | $3.357,58 |
| HD | -$4.491,7 | -$5.002,76 | -$4.843,12 | $2.520,49 |
| BAC | -$4.641,57 | -$4.017,49 | -$2.588,89 | $5.880,18 |
| PFE | -$3.913,79 | -$3.236,17 | -$4.358,06 | $3.252,18 |
| WFC | $309,97 | -$3.488,26 | -$6.321,32 | $6.627,38 |
| CVX | $1.686,49 | -$903,09 | $5.414,68 | $9.172,12 |
| UTX | $1.132,83 | $301,21 | -$1.690,97 | $5.169,85 |
| MDT | $1.543,71 | $81,96 | -$3.058,66 | $5.608,06 |
| HON | -$138,26 | -$366,97 | $147,02 | $6.283,95 |
| BMY | -$1.934,93 | -$1.997,37 | -$2.820,40 | $5.111,98 |
| BA | $14,22 | $2.171,52 | -$1.990,97 | $6.615,65 |
| IBM | $702,70 | -$593,99 | -$367,11 | $5.488,49 |
| WMT | $410,02 | -$2.501,45 | -$1.724,35 | $6.359,24 |
| AAPL | $31.114,37 | $17.420,48 | $26.956,85 | $97.776,72 |
| MSFT | -$1.231,96 | -$4.080,51 | -$674,72 | $8.067,93 |
| BRKB | $4.642,86 | $2.359,40 | -$2.075,03 | $8.411,10 |
| MA | $12.182,20 | $9.519,22 | $2.831,36 | $21.774,12 |
| DIS | $674,97 | $2.110,20 | -$818,91 | $1.479,87 |
| V | $4.439,16 | $4.203,69 | -$2.030,36 | $8.327,75 |
| MMM | -$2.045,36 | -$3.388,90 | -$2.325,36 | $2.073,84 |
| PM | $8.102,11 | $3.265,02 | $2.208,59 | $13.333,25 |
| INTC | -$1.856,66 | -$1.277,88 | -$830,56 | $4.716,03 |
| CSCO | $74,87 | -$1.609,55 | -$3.946,78 | $8.631,76 |
| PG | $2.500,00 | -$991,19 | -$934,31 | $8.266,96 |
| GOOGL | -$1.031,18 | -$230,00 | $2.288,33 | $10.551,24 |
| UNP | $9.815,55 | $1.029,44 | $2.830,19 | $18.177,28 |
| JNJ | $1.038,69 | -$641,97 | $20,70 | $0,00 |
| MRK | -$278,32 | $759,97 | -$2.167,89 | $13.128,04 |
| XOM | $5.746,22 | $2.277,44 | -$771,99 | $6.934,31 |
| MO | -$6.182,24 | $616,95 | -$8.350,84 | $2.346,59 |
| AMZN | $6.610,64 | $5.827,54 | $6.074,77 | $35.389,87 |
| ABBV | $2.900,97 | $3.322,96 | $1.512,46 | $5.227,56 |
| GILD | $11.832,06 | $8.258,70 | -$5.391,78 | $22.280,68 |
| ORCL | $3.631,19 | $1.747,77 | -$1.572,96 | $8.642,77 |
| FB | $18.046,26 | $4.560,36 | $2.071,40 | $23.657,48 |
| C | -$6.524,43 | -$2.595 | -$5.441,80 | $8.239,60 |
| CVS | $3.344,02 | $833,63 | -$3.662,15 | $13.220,15 |
| PEP | $3.235,77 | $1.406,87 | -$159,01 | $6.692,48 |
| JPM | $352,82 | -$3.378,22 | -$4.968,51 | $12.836,16 |
Table 4.5 shows values for test statistics \(W\) and corresponding p-values. If we focus on the test phase, obtained p-values are much smaller than \(0.05\) for all three popular models. This means that there is a statistically significant difference between the resulting yields achieved by our proposed model and existing three models. For the test phase we can conclude with a high level of confidence that appropriately parametrised proposed model W2V performed better than existing three models. As mentioned earlier, the proposed method achieved worse results in the validation phase. In the validation phase the difference in returns between the proposed model and reference models was statistically significant only for MACD and MA. Comparing to MACD, we obtained p-value smaller \(0.0001\), which means that our model yields better results. Similar results are obtained when comparing W2V to MA(50, 100).
| W | p-value | W | p-value | |
|---|---|---|---|---|
| Buy & Hold | 2 | < 0,0001 | ||
| MA(50, 100) | 1 | < 0,0001 | 427 | 0.021 |
| MACD | 1 | < 0,0001 | 155 | < 0,0001 |
The p-value was \(0.021\), which is more than half that of the limit of \(p = 0.05\), where the hypothesis could not be confirmed. When compared to Buy & Hold, the W2V method yields lower returns. That can be seen already from the average yields in Table 4.3. To prove that Buy & Hold gives statistically better results compared to W2V method, we performed additional Wilcoxon Signed Rank t-test, and obtained a p-value of less than \(0.0001\).
Given the presented results, we can conclude that if the model parameters are well set, presented forecast model gives better results than presented popular models. However, the parameters that perform well in the test phase may not perform equally well in the later validation phase.
5 Conclusion and Future Work
Stock trend forecasting is a challenging task and has become an attractive topic during the last few decades. In this paper, we present a novel approach for stock trend prediction. Besides focusing on prediction accuracy, the presented approach was also tested for financial success. In the test phase, we used three sample stocks – Apple (AAPL), Coca-Cola (KO) and Microsoft (MSFT) – that satisfied conditions for a good test case (the stock trend diverse in observed period, known company’s business model, enough data available). The confirmation analysis was performed with analysis on Russell Top 50 Index.
We realized that even if the forecasting model has high prediction accuracy, it can still achieve bogus financial yields, if poor trading strategy is used. However, despite the simplicity of the proposed model’s trading strategy, its performance was very good with a statistical significance.
In the test phase, the proposed model performed well for all three sample stocks. The yields were higher than the yields of the comparative models, i.e., Buy & Hold, MA and MACD. In the validation phase, the proposed model outperformed MA and MACD models, while the Buy & Hold turned out to be statistically most profitable. In more extensive testing on Russell Top 50 Index, the proposed method was outperformed only by Buy & Hold, while achieved statistically better average yields than MA and MACD.
A more detailed analysis of trading graphs and statistical analysis showed that the proposed model has a great potential for practical use. However, it is too early to conclude that the proposed model provides a financial gain, as we have shown that selected model parameters are not equally appropriate for different time periods in terms of yield. We have also shown that the forecast model is strongly influenced by the training data set. If the model is trained with data that contains bear trend, the predictive model might be very cautious despite the general growth trend of validation data set. The problem is due to over-fitting, so training with more data would help. Some of the state-of-art machine learning algorithms like Word2Vec are dependent on a large-scale data set to become more efficient and eliminate the risk of over-fitting.
We hope that the proposed approach can offer some beneficial contributions to a stock trend prediction and can serve as a motivation for further research. In the future, we would like to improve method’s trading strategy and incorporate the stop loss function and some other proven, often used technical indicators. In the training phase, we could include OHLC data of other stocks to acquire more diverse patterns, reducing unknown ones. That would help algorithms to identify the underlying future chart pattern better. To improve classification accuracy and logarithmic loss, the SoftMax regression could be replaced with advanced machine learning classification algorithms. It is also worth exploring, how candlestick data with different time grains affect prediction accuracy. This way we could compare daily, weekly or monthly trend forecasts.
References
Abad, Cristina, Sten A Thore, and Joaquina Laffarga. 2004. “Fundamental Analysis of Stocks by Two-Stage DEA.” Managerial and Decision Economics 25 (5): 231–41. doi:10.1002/mde.1145.
Ballings, Michel, Dirk Van den Poel, Nathalie Hespeels, and Ruben Gryp. 2015. “Evaluating Multiple Classifiers for Stock Price Direction Prediction.” Expert Systems with Applications 42 (20): 7046–56. doi:10.1016/j.eswa.2015.05.013.
Cavalcante, Rodolfo C., Rodrigo C. Brasileiro, Victor L. F. Souza, Jarley P. Nobrega, and Adriano L. I. Oliveira. 2016. “Computational Intelligence and Financial Markets: A Survey and Future Directions.” Expert Systems with Applications 55: 194–211. doi:10.1016/j.eswa.2016.02.006.
Fama, Eugene F. 1960. “Efficient Markets Hypothesis.” PhD Thesis, Ph. D. dissertation, University of Chicago Graduate School of Business.
Hafezi, Reza, Jamal Shahrabi, and Esmaeil Hadavandi. 2015. “A Bat-Neural Network Multi-Agent System (BNNMAS) for Stock Price Prediction: Case Study of DAX Stock Price.” Applied Soft Computing 29: 196–210. doi:10.1016/j.asoc.2014.12.028.
Huang, Wei, Yoshiteru Nakamori, and Shou-Yang Wang. 2005. “Forecasting Stock Market Movement Direction with Support Vector Machine.” Computers & Operations Research 32 (10): 2513–22. doi:10.1016/j.cor.2004.03.016.
Jasemi, Milad, Ali M Kimiagari, and A Memariani. 2011. “A Modern Neural Network Model to Do Stock Market Timing on the Basis of the Ancient Investment Technique of Japanese Candlestick.” Expert Systems with Applications 38 (4): 3884–90. doi:10.1016/j.eswa.2010.09.049.
Kamo, Takenori, and Cihan Dagli. 2009. “Hybrid Approach to the Japanese Candlestick Method for Financial Forecasting.” Expert Systems with Applications 36 (3): 5023–30. doi:10.1016/j.eswa.2008.06.050.
Keogh, Eamonn, and Jessica Lin. 2005. “Clustering of Time-Series Subsequences Is Meaningless: Implications for Previous and Future Research.” Knowledge and Information Systems 8 (2): 154–77. doi:10.1007/s10115-004-0172-7.
Kumar, Manish, and M. Thenmozhi. 2006. “Forecasting Stock Index Movement: A Comparison of Support Vector Machines and Random Forest.” SSRN Scholarly Paper ID 876544. Rochester, NY: Social Science Research Network. https://papers.ssrn.com/abstract=876544.
Liu, Fajiang, and Jun Wang. 2012. “Fluctuation Prediction of Stock Market Index by Legendre Neural Network with Random Time Strength Function.” Neurocomputing 83: 12–21. doi:10.1016/j.neucom.2011.09.033.
Lu, Chi-Jie, and Jui-Yu Wu. 2011. “An Efficient CMAC Neural Network for Stock Index Forecasting.” Expert Systems with Applications 38 (12): 15194–15201. doi:10.1016/j.eswa.2011.05.082.
Lu, Chi-Jie, Tian-Shyug Lee, and Chih-Chou Chiu. 2009. “Financial Time Series Forecasting Using Independent Component Analysis and Support Vector Regression.” Decision Support Systems 47 (2): 115–25. doi:10.1016/j.dss.2009.02.001.
Lu, Tsung-Hsun. 2014. “The Profitability of Candlestick Charting in the Taiwan Stock Market.” Pacific-Basin Finance Journal 26: 65–78. doi:10.1016/j.pacfin.2013.10.006.
Lu, Tsung-Hsun, and Yung-Ming Shiu. 2012. “Tests for Two-Day Candlestick Patterns in the Emerging Equity Market of Taiwan.” Emerging Markets Finance and Trade 48 (sup1): 41–57. doi:10.2753/REE1540-496X4801S104.
Malkiel, Burton G. 2003. “The Efficient Market Hypothesis and Its Critics.” Journal of Economic Perspectives 17 (1): 59–82. doi:10.1257/089533003321164958.
Martinez, L. C., D. N. da Hora, J. R. de M. Palotti, W. Meira, and G. L. Pappa. 2009. “From an Artificial Neural Network to a Stock Market Day-Trading System: A Case Study on the BM Amp;F BOVESPA.” In 2009 International Joint Conference on Neural Networks, 2006–13. doi:10.1109/IJCNN.2009.5179050.
Martiny, Karsten. 2012. “Unsupervised Discovery of Significant Candlestick Patterns for Forecasting Security Price Movements.” In KDIR, 145–50.
Mikolov, Tomas, Kai Chen, Greg Corrado, and Jeffrey Dean. 2013. “Efficient Estimation of Word Representations in Vector Space.” arXiv Preprint arXiv:1301.3781.
Mikolov, Tomas, Ilya Sutskever, Kai Chen, Greg S Corrado, and Jeff Dean. 2013. “Distributed Representations of Words and Phrases and Their Compositionality.” In Advances in Neural Information Processing Systems, 3111–9.
Mikolov, Tomas, Wen-tau Yih, and Geoffrey Zweig. 2013. “Linguistic Regularities in Continuous Space Word Representations.” In Proceedings of the 2013 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, 746–51.
Nison, S. 1991. Japanese Candlestick Charting Techniques: A Contemporary Guide to the Ancient Investment Techniques of the Far East. New York Institute of Finance.
Prado, Hércules A do, Edilson Ferneda, Luis CR Morais, Alfredo JB Luiz, and Eduardo Matsura. 2013. “On the Effectiveness of Candlestick Chart Analysis for the Brazilian Stock Market.” Procedia Computer Science 22: 1136–45.
Rousseeuw, Peter J. 1987. “Silhouettes: A Graphical Aid to the Interpretation and Validation of Cluster Analysis.” Journal of Computational and Applied Mathematics 20: 53–65.
Savić, Boris. 2016. “Tvorba Jezika Japonskih Svečnikov in Uporaba NLP Algoritma Word2Vec Za Napovedovanje Trendov Gibanja Vrednosti Delnic.” Master’s thesis, Ljubljana, Slovenia: University of Ljubljana, Faculty of Computer; Information Science. http://eprints.fri.uni-lj.si/3664/.
Tay, Francis E. H., and Lijuan Cao. 2001. “Application of Support Vector Machines in Financial Time Series Forecasting.” Omega 29 (4): 309–17. doi:10.1016/S0305-0483(01)00026-3.
Taylor, Mark P, and Helen Allen. 1992. “The Use of Technical Analysis in the Foreign Exchange Market.” Journal of International Money and Finance 11 (3): 304–14. doi:10.1016/0261-5606(92)90048-3.
Teixeira, Lamartine Almeida, and Adriano Lorena Inácio de Oliveira. 2010. “A Method for Automatic Stock Trading Combining Technical Analysis and Nearest Neighbor Classification.” Expert Systems with Applications 37 (10): 6885–90. doi:10.1016/j.eswa.2010.03.033.
Tsinaslanidis, Prodromos E., and Dimitris Kugiumtzis. 2014. “A Prediction Scheme Using Perceptually Important Points and Dynamic Time Warping.” Expert Systems with Applications 41 (15): 6848–60. doi:10.1016/j.eswa.2014.04.028.
Wang, Jie, and Jun Wang. 2015. “Forecasting Stock Market Indexes Using Principle Component Analysis and Stochastic Time Effective Neural Networks.” Neurocomputing 156: 68–78. doi:10.1016/j.neucom.2014.12.084.
Zhang, Dongwen, Hua Xu, Zengcai Su, and Yunfeng Xu. 2015. “Chinese Comments Sentiment Classification Based on Word2vec and SVMperf.” Expert Systems with Applications 42 (4): 1857–63. doi:10.1016/j.eswa.2014.09.011.